문제

문제이해
조합 ( nCr )
조합이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 없음)
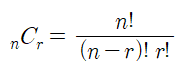
이렇게 풀면 시간초과가 나옵니다.
도저히 다른 방법이 생각이 안났습니다. 다른 사람 풀이의 힌트를 보았고 0의 개수를 출력한다는 것은 10의 배수를 측정하는 것과 같았습니다.
그렇다면 m!과 n!, (m-n)!의 2의 개수와 5의 개수를 구하면 됩니다.
하지만 다시 팩토리얼을 돌면 시간초과가 날것이니 다른 방법이 필요 합니다.
25! = 15511210043330985984000000 입니다.
10의 배수는 6개 있죠. 2와5는 무조건 6쌍을 필요로 합니다.
즉, 한 숫자 팩토리얼의 5의 개수를 알고 싶다면 몫을 계속 5로 0이 될 때 까지 수를 저장합니다.
ex) 25 => [ 5 ] => [ 1 ] => [ 0 ]
25의 5의배수 개수 = 5+1+0 = 6
한 숫자 팩토리얼의 2의 개수를 알고 싶다면 몫을 계속 2로 0이 될 때 까지 수를 저장합니다.
ex)25 => [ 12 ] => [ 6 ] => [ 3 ] => [ 1 ] =>[ 0 ]
25의 2의배수 개수 = 12+6+3+1 = 22
왜 25의 5의배수 개수는 5개가 아니라 6개일까?
예를 들어, 500이라는 수는 5의 배수가 100개, 25의 배수가 20개, 125의 배수가 4개 이므로,
500!의 뒤에서부터 처음으로 0이 아닌 다른 수가 나올때까지 0의 개수는 100+20+4=124가 된다.
(125, 25의 배수는 각각 5의 배수에 포함되지만, 5의 배수를 셀 때 한 번씩만 카운트하게 된다.
하지만, 사실 25는 2번, 125는 3번 세야하므로, 25, 125의 배수의 개수를 그대로 구하여 더해주어야한다.
위와 같이 500이라는 수에서 5의 배수는 100개 나왔을 때, 25, 125의 배수는 각각 한번, 두번 더 세어주어야 한다.
여기서 25의 배수를 한번 더 더해주면, 125의 배수만 한번 더 카운트 해주어야 하므로,
125의 배수까지 카운트 해주면 모두 알맞게 더한 것이 된다.)
즉, 5의 배수의 개수 + 25의 배수의 개수 + 125의 배수의 개수가 주어진 수 N!의 0의 개수가 된다.
(N은 0~500사이의 수 이므로, 5의 네제곱인 625부터는 포함하지 않았다.)
5의 개수 6개, 2의 개수 22개 가 답으로 나왔고 우리는 6개가 꼭 필요하니 10의 배수는 6개라고 알 수 있습니다. 0의 개수는 6개입니다.
이렇게 한 팩토리얼의 2,5의 개수를 알 수 있으니 최종적으로 { 25,12 }를 살펴봐야 합니다.
0의개수
=
M!가 가지고 있는 2의 개수 - N!이 가지고 있는 2의 개수 - (M-N)!이 가지고 있는 2의 개수
/
M!가 가지고 있는 5의 개수 - N!이 가지고 있는 5의 개수 - (M-N)!이 가지고 있는 5의 개수
중에 작은 수
왜 이런식이 나오냐면 2,5의 개수는 지수 형태로 나타낼 수 있습니다.
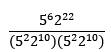
이렇게 나누기 형태로 나오기 때문에 지수의 차를 이용할 수 있습니다.
코드
n,m = map(int, input().split())
def count_5(x):
count = 0
while(x !=0):
x = x//5 #몫은 개수 이다.
count += x
return count
def count_2(x):
count = 0
while(x !=0):
x = x//2 #몫은 개수 이다.
count += x
return count
result_5=count_5(n) - count_5(m) - count_5(n-m)
result_2=count_2(n) - count_2(m) - count_2(n-m)
print(min(result_2,result_5))2와 5의 개수, 짝을 맞춰야 10이 되니 가장 작은 수가 곧 10의 개수가 됩니다.
참고
https://beginnerdeveloper-lit.tistory.com/18 [초보 개발자의 이야기, 릿허브]
https://somjang.tistory.com/entry/BaeKJoon-2004번-조합-0의-개수-Python [솜씨좋은장씨]
'알고리즘 > 백준알고리즘' 카테고리의 다른 글
| [백준 알고리즘/Python] 1373 2진수 8진수 (0) | 2022.01.24 |
|---|---|
| [백준 알고리즘/Python] 17087 숨박꼭질6 (0) | 2022.01.23 |
| [백준 알고리즘/Python] 1676 팩터리얼 0의 개수 (0) | 2022.01.19 |
| [백준 알고리즘/Python] 6588 골드바흐의 추측 (0) | 2022.01.18 |
| [백준 알고리즘/Java] 2609 최대공약수와 최소공배수 (0) | 2022.01.13 |



